PhiLambda: agosto 2020

PRIMORFISMOS Y PERMUTACIONES ÁUREAS: UN NUEVO TEOREMA DE IDENTIFICACIÓN DIGITAL ÁUREA PRIMA

JAVIER GRISALES HERRERA

19/08/20

JAVIER GRISALES HERRERA se distribuye bajo una Licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional.

Girando en arcos dorados van los dodecaprimos e icosaprimos en 8 rotaciones isométricas. Sus medidas son segmentos áureos en politopos. 12 horas, 12 notas musicales, 12 signos del zodiaco que son los 12 sectores de 30° de la eclíptica desde el equinoccio vernal, una de las intersecciones con la elíptica con el ecuador celeste, conocido como punto Aries, que es el punto de la eclíptica a partir del cual el Sol pasa del hemisferio sur celeste al hemisferio norte, lo que ocurre en el equinoccio de marzo (iniciando así la primavera en el hemisferio norte y el otoño en el hemisferio sur).

12 runas solares, 12 runas lunares, 12th Fibonacci's.

Los números primos son las huellas que se borran en la nieve de un gigante desaparecido en un camino indeterminado todavía, representan aparentemente una profunda falla estructural en el castillo matemático de puntos, segmentos y magnitudes, un abismo insondable hasta ahora. Pero, ¿son realmente segmentos de código aleatorio disperso en la recta real que crean una suerte de orden no lineal propio en sistemas estocásticos? Aunque Zp sea un cuerpo algebraico con p primo, ¿la estructura algebraica de sus elementos no permite la identificación de un primo P_n dada su ordinalidad y viceversa? ¿No se puede crear un localizador para determinar el nombre y dirección de cada uno? En este artículo número 12 voy a mostrar la existencia de 8 familias áureas primas que particionan a todo el conjunto primo. De esta manera, pueden ser rastreadas las huellas del gigante primo.

En mi segundo artículo probé la existencia de 4 familias áureas primas obtenidas a partir de los períodos recíprocos decimales de 1/p. Estas familias son 4 clases residuales módulo 90, que son: 18°,36°,54°,72°. Cada clase residual indica una familia de primos según su último digito. De la siguiente manera:

{P₁, P₃, P₇, P₉} ↔ {18°,36°,54°,72°}

https://www.wolframalpha.com/input/?i=Table+%5B+%282%28prime%28n%29%29%5E%28-1%29%2810%5E%28prime%28n%29-1%29+-1%29%29+mod+90%2C+%7B+n%2C+4%2C+300%2C+1+%7D+%5D

Ahora voy a mostrar un nuevo resultado, que permanecía oculto en estas 4 clases residuales.

TEOREMA DE IDENTIFICACIÓN DIGITAL ÁUREA PRIMA

Proposición 1:

El módulo 360 de la doble expansión decimal recíproca de p primo, arroja como resultado 8 clases residuales o ángulos áureos únicos. Estas clases residuales agrupan 8 familias primas disjuntas. Así, se puede realizar un rastreo digital de cada primo dado a partir de su ordinal.

P₁ ↔ {18°, 198°}

P₃ ↔ {126°, 306°}

P₇ ↔ {54°, 234°}

P₉ ↔ {162°, 342°}

https://www.wolframalpha.com/input/?i=Table+%5B+%282%28prime%28n%29%29%5E%28-1%29%2810%5E%28prime%28n%29-1%29+-1%29%29+mod+360%2C+%7B+n%2C+4%2C+300%2C+1+%7D+%5D

https://www.wolframalpha.com/input/?i=Table+%5B+12%5En+mod+360%2C+%7B+n%2C+2%2C+200%2C+1+%7D+%5D

https://www.wolframalpha.com/input/?i=Table+%5B+2+3%5En+mod+360%2C+%7B+n%2C+2%2C+200%2C+1+%7D+%5D

Proposición 2:

Basado en las 8 isometrías áureas primas módulo 360, se puede identificar exactamente el último dígito y la paridad del penúltimo dígito de cualquier primo Pj. Así, tenemos los primos penultimpares y penultipares.

PRIMOS PENULTIMPARES:

Son aquellos primos cuyo penúltimo dígito es un número impar. Estos primos tienen 4 clases residuales módulo 360 y son los ángulos: 18°,54°,126°,162°. Estos primos siempre dan ángulos que se encuentran en el primer y segundo cuadrante del plano cartesiano 0°< θ < 180°.

P₁ ↔ {18°}

11,31,71,131,151,191,211,251,271,311,331,431,491,571,631,691,751,811,911, 971…

P₃ ↔ {126°}

13,53,73,113,173,193,233,293,313,353,373,433,593,613,653,673,733,773,853, 953…

P₇ ↔ {54°}

17,37,97,137,157,197,257,277,317,337,397,457,557,577,617,677,757,797,857, 877,937,977,997…

P₉ ↔ {162°}

19,59,79,139,179,199,239,359,379,419,439,479,499,599,619,659,719,739,839, 859,919…

https://www.wolframalpha.com/input/?i=%5B+%282%28%2811%29%29%5E%28-1%29%2810%5E%28%2811%29-1%29+-1%29%29%2C++%282%28%28251%29%29%5E%28-1%29%2810%5E%28%28251%29-1%29+-1%29%29%2C++%282%28%28911%29%29%5E%28-1%29%2810%5E%28%28911%29-1%29+-1%29%29%2C+%282%28%28211%29%29%5E%28-1%29%2810%5E%28%28211%29-1%29+-1%29%29+%5D+mod360+

https://www.wolframalpha.com/input/?i=%5B+%282%28%28113%29%29%5E%28-1%29%2810%5E%28%28113%29-1%29+-1%29%29%2C++%282%28%2853%29%29%5E%28-1%29%2810%5E%28%2853%29-1%29+-1%29%29%2C++%282%28%2813%29%29%5E%28-1%29%2810%5E%28%2813%29-1%29+-1%29%29%2C+%282%28%28233%29%29%5E%28-1%29%2810%5E%28%28233%29-1%29+-1%29%29+%5D+mod360+

https://www.wolframalpha.com/input/?i=%5B+%282%28%2817%29%29%5E%28-1%29%2810%5E%28%2817%29-1%29+-1%29%29%2C++%282%28%2837%29%29%5E%28-1%29%2810%5E%28%2837%29-1%29+-1%29%29%2C++%282%28%28137%29%29%5E%28-1%29%2810%5E%28%28137%29-1%29+-1%29%29%2C+%282%28%28977%29%29%5E%28-1%29%2810%5E%28%28977%29-1%29+-1%29%29+%5D+mod360+

https://www.wolframalpha.com/input/?i=%5B+%282%28%28419%29%29%5E%28-1%29%2810%5E%28%28419%29-1%29+-1%29%29%2C++%282%28%28859%29%29%5E%28-1%29%2810%5E%28%28859%29-1%29+-1%29%29%2C++%282%28%28139%29%29%5E%28-1%29%2810%5E%28%28139%29-1%29+-1%29%29%2C+%282%28%2879%29%29%5E%28-1%29%2810%5E%28%2879%29-1%29+-1%29%29+%5D+mod360+

PRIMOS PENULTIPARES:

Son aquellos primos cuyo penúltimo dígito es un número par. Estos primos tienen 4 clases residuales módulo 360 y son los ángulos: 198°,234°,306°,342°. Estos primos siempre dan ángulos que se encuentran en el tercer y cuarto cuadrante del plano cartesiano 180°< θ < 360°.

P₁ ↔ {198°}

41,61,101,181,241,281,401,421,461,521,541,601,641,661,701,761,821,881,941…

P₃ ↔ {306°}

23,43,83,103,163,223,263,283,383,443,463,503,523,563,643,683,743,823,863, 883,983…

P₇ ↔ {234°}

07,47,67,107,127,167,227,307,347,367,467,487,547,587,607,647,727,787,827, 887,907,947,967…

P₉ ↔ {342°}

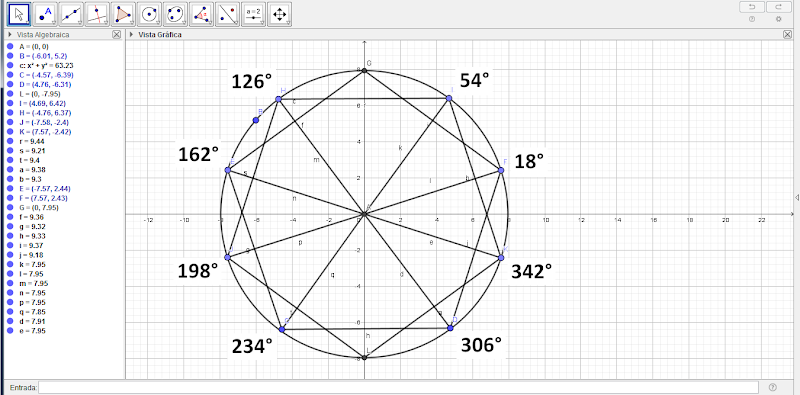
29,89,109,149,229,269,349,389,409,449,509,569,709,769,809,829,929…

Aquí las 8 subclases áureas primas:

https://www.wolframalpha.com/input/?i=%5B+%282%28%2841%29%29%5E%28-1%29%2810%5E%28%2841%29-1%29+-1%29%29%2C++%282%28%2861%29%29%5E%28-1%29%2810%5E%28%2861%29-1%29+-1%29%29%2C++%282%28%28421%29%29%5E%28-1%29%2810%5E%28%28421%29-1%29+-1%29%29%2C+%282%28%28661%29%29%5E%28-1%29%2810%5E%28%28661%29-1%29+-1%29%29+%5D+mod360+

https://www.wolframalpha.com/input/?i=%5B+%282%28%2823%29%29%5E%28-1%29%2810%5E%28%2823%29-1%29+-1%29%29%2C++%282%28%2843%29%29%5E%28-1%29%2810%5E%28%2843%29-1%29+-1%29%29%2C++%282%28%28103%29%29%5E%28-1%29%2810%5E%28%28103%29-1%29+-1%29%29%2C+%282%28%28983%29%29%5E%28-1%29%2810%5E%28%28983%29-1%29+-1%29%29+%5D+mod360+

https://www.wolframalpha.com/input/?i=%5B+%282%28%28367%29%29%5E%28-1%29%2810%5E%28%28367%29-1%29+-1%29%29%2C++%282%28%28827%29%29%5E%28-1%29%2810%5E%28%28827%29-1%29+-1%29%29%2C++%282%28%28947%29%29%5E%28-1%29%2810%5E%28%28947%29-1%29+-1%29%29%2C+%282%28%2867%29%29%5E%28-1%29%2810%5E%28%2867%29-1%29+-1%29%29+%5D+mod360+

https://www.wolframalpha.com/input/?i=%5B+%282%28%28109%29%29%5E%28-1%29%2810%5E%28%28109%29-1%29+-1%29%29%2C++%282%28%28389%29%29%5E%28-1%29%2810%5E%28%28389%29-1%29+-1%29%29%2C++%282%28%28769%29%29%5E%28-1%29%2810%5E%28%28769%29-1%29+-1%29%29%2C+%282%28%28929%29%29%5E%28-1%29%2810%5E%28%28929%29-1%29+-1%29%29+%5D+mod360+

En definitiva, los primorfismos áureos o isomorfismos primos envían primos en segmentos áureos y conservan la estructura con la suma y el producto algebraico. Estas clases residuales módulo 360 son permutaciones de las isometrías del pentágono regular rotadas +18° y -18° en la circunferencia trigonométrica.

( P₁, P₉) = ( φ^-1, φ^-1 ) ↔ Penúltimo dígito impar

( P₁, P₉) = ( -φ^-1, -φ^-1 ) ↔ Penúltimo dígito par

( P₃, P₇) = ( φ , φ ) ↔ Penúltimo dígito impar

( P₃, P₇) = ( -φ , -φ ) ↔ Penúltimo dígito par

TEOREMA DEL COCIENTE ÁUREO DE CLASES PRIMAS

Proposición 1:

Sea F(x) una función compleja expresada como la raíz del cociente senoidal de las 4 clases primas divididas en 8 subclases (4 pares y 4 impares en su penúltimo digito), tiene como conjunto imagen 6 raíces áureas: { 1, , φ, φ^-1, i, φi, iφ^-1}

Analizando, vemos que son 3 raíces reales y 3 raíces complejas. Pero, ¿Cómo vienen determinadas dichas imágenes según sus preimágenes? De la siguiente manera: P_n(par)y P_m(impar), donde n=1,3,7,9 y m=1,3,7,9. Que son el último dígito de cualquier primo p>5.

Si el primo P_n del numerador y el primo P_m del denominador tienen ambos como penúltimo dígito un número par o impar, entonces la imagen es real: 1, φ, φ^-1

https://www.wolframalpha.com/input/?i=root+%28Sin+%5B%282%28%2813%29%29%5E%28-1%29%2810%5E%28%2813%29-1%29+-1%29%29%5D%C2%B0+%2F+Sin+%5B%282%28%2879%29%29%5E%28-1%29%2810%5E%28%2879%29-1%29+-1%29%29%5D%C2%B0%29

Si el primo P_n del numerador y el primo P_m del denominador tienen como penúltimo dígito números pares e impares, entonces la imagen es imaginaria: i, φi, iφ^-1

https://www.wolframalpha.com/input/?i=root+%28Sin+%5B%282%28%2823%29%29%5E%28-1%29%2810%5E%28%2823%29-1%29+-1%29%29%5D%C2%B0+%2F+Sin+%5B%282%28%2819%29%29%5E%28-1%29%2810%5E%28%2819%29-1%29+-1%29%29%5D%C2%B0%29

Las combinaciones son las siguientes:

P₁↔ P1 = 1, i

P₁↔ P₃ = φ^-1, iφ^-1

P₁↔ P₇ = φ^-1, iφ^-1

P₁↔ P₉ = 1, i

P₃↔ P₁ = φ, iφ

P₃↔ P₃ = 1, i

P₃↔ P₇ = 1, i

P₃↔ P₉ = φ, iφ

P₇↔ P₁ = φ, iφ

P₇↔ P₃ = 1, i

P₇↔ P₇ = 1, i

P₇↔ P₉ = φ, iφ

P₉↔ P₁ = 1, i

P₉↔ P₃ = φ^-1, iφ^-1

P₉↔ P₇ = φ^-1, iφ^-1

P₉↔ F₉ = 1, i

Ver acá y acá en Wolfram:

https://www.wolframalpha.com/input/?i=root+%28Sin+%5B%282%28%2811%29%29%5E%28-1%29%2810%5E%28%2811%29-1%29+-1%29%29%5D%C2%B0+%2F+Sin+%5B%282%28%2817%29%29%5E%28-1%29%2810%5E%28%2817%29-1%29+-1%29%29%5D%C2%B0%29

Proposición 2:

Sea F(x) una función real expresada como el cociente cosenoidal de las 4 clases primas divididas en 8 subclases (4 pares y 4 impares en su penúltimo digito), tiene como conjunto imagen 6 raíces áureas: { 1, φ, φ^-1, -1, -φ, -φ^-1}

Se obtienen valores negativos al hacer el cociente de clases primas residuales izquierdas (126°,162°,198°,234°) con clases primas derechas (18°,54°,306°,342°). Las imágenes son: -1, -φ, -φ^-1

https://www.wolframalpha.com/input/?i=Cos%282%28%2889%29%29%5E%28-1%29%2810%5E%28%2889%29-1%29+-1%29%29%C2%B0+%2F+Cos%282%28%28107%29%29%5E%28-1%29%2810%5E%28%28107%29-1%29+-1%29%29%C2%B0+

Se obtienen valores positivos al hacer el cociente de clases primas residuales solo derechas o solo izquierdas. Las imágenes son: 1, φ, φ^-1

https://www.wolframalpha.com/input/?i=Cos%282%28%2819%29%29%5E%28-1%29%2810%5E%28%2819%29-1%29+-1%29%29%C2%B0+%2F+Cos%282%28%28107%29%29%5E%28-1%29%2810%5E%28%28107%29-1%29+-1%29%29%C2%B0+

Las combinaciones son las siguientes:

P₁↔ P1 = 1, -1

P₁↔ P₃ = φ, -φ

P₁↔ P₇ = φ, -φ

P₁↔ P₉ = 1, -1

P₃↔ P₁ = φ^-1, -φ^-1