SIMETRÍA ÁUREA PRIMA: UN ÁLGEBRA DORADA CICLOTÓMICA
JAVIER GRISALES HERRERA
13/03/21
La verdad es la
intersección entre los hechos y las teorías.
La verdad es hija del
tiempo (Veritas filia temporis), no de la autoridad. Francis Bacon
El grupo real SO(n) es
un grupo de Lie y es un subgrupo del grupo ortogonal O(n). Este subgrupo SO(n)
se puede identificar con el grupo de rotaciones del espacio Rn.
Veamos el caso para una rotación r en R2
Las 8 clases primas corresponden a los ceros del polinomio ciclotómico número
20:
{i1/5, i3/5, i7/5, i9/5 ,i-1/5, i-3/5, i-7/5, i-9/5}
https://www.wolframalpha.com/input/?i=e%5E%28ipi%2F10%29+%3D+i%5E%281%2F5%29
https://www.wolframalpha.com/input/?i=e%5E%283i%CF%80%2F10%29+%3D+i%5E%283%2F5%29
https://www.wolframalpha.com/input/?i=e%5E%287i%CF%80%2F10%29+%3D+i%5E%287%2F5%29
https://www.wolframalpha.com/input/?i=e%5E%289i%CF%80%2F10%29+%3D+i%5E%289%2F5%29
Ahora veamos la forma trigonométrica
de dichas raíces quintas de i
https://www.wolframalpha.com/input/?i=+i%5E%281%2F5%29+%3D+cos18+%2B+i+sin18
https://www.wolframalpha.com/input/?i=+i%5E%283%2F5%29+%3D+cos54+%2B+i+sin54
https://www.wolframalpha.com/input/?i=+i%5E%287%2F5%29+%3D+cos126+%2B+i+sin126
https://www.wolframalpha.com/input/?i=+i%5E%289%2F5%29+%3D+cos162+%2B+i+sin162
En el tercer y cuarto
cuadrante:
https://www.wolframalpha.com/input/?i=+i%5E%28-1%2F5%29+%3D+cos%28-18%29%2B+i+sin%28-18%29
https://www.wolframalpha.com/input/?i=+i%5E%28-3%2F5%29+%3D+cos%28-54%29%2B+i+sin%28-54%29
https://www.wolframalpha.com/input/?i=+i%5E%28-7%2F5%29+%3D+cos%28-126%29%2B+i+sin%28-126%29
https://www.wolframalpha.com/input/?i=+i%5E%28-9%2F5%29+%3D+cos%28-162%29%2B+i+sin%28-162%29
ISOMETRÍAS PRIMAS EN RADIANES:
18°
↔ π/10
54° ↔ 3π/10
126° ↔ 7π/10
162° ↔ 9π/10
198° ↔ 11π/10 ↔ -162° ↔ -9π/10
234° ↔ 13π/10 ↔ -126° ↔ -7π/10
306° ↔ 17π/10 ↔ -54° ↔ -3π/10
342° ↔ 19π/10 ↔ -18° ↔ -π/10
IGUALDAD ENTRE LAS RAÍCES COMPLEJAS
i-1/5 =
-i9/5
i-3/5 =
-i7/5
i-7/5 =
-i3/5
i-9/5 =
-i1/5
https://www.wolframalpha.com/input/?i=i%5E%28-1%2F5%29+%3D+-i%5E%289%2F5%29
https://www.wolframalpha.com/input/?i=i%5E%28-3%2F5%29+%3D+-i%5E%287%2F5%29
https://www.wolframalpha.com/input/?i=i%5E%28-7%2F5%29+%3D+-i%5E%283%2F5%29
https://www.wolframalpha.com/input/?i=i%5E%28-9%2F5%29+%3D+-i%5E%281%2F5%29
PROPOSICIÓN PARA LOS COSENOS:
Cos18° = Cos342° = 0.9510…
Cos162° = Cos198°
= -0.9510…
Y en general:
Cos [ 2 32n
]° =
0.9510…si n es
impar =
[ root(2+φ) ] / 2
-0.9510…si n es
par = - [
root(2+φ) ] / 2
https://www.wolframalpha.com/input/?i=%5B+root%282%2B%CF%86%29+%5D+%2F+2
Cos54° = Cos306° = 0.5877…
Cos126° = Cos234°
= -0.5877…
Y en general:
Cos [ 2 32n+1
]° =
0.5877…si n es
impar =
[ root(2 - φ-1) ] / 2
-0.5877…si n es
par = - [ root(2 - φ-1) ]
/ 2
https://www.wolframalpha.com/input/?i=%5B+root%282-%CF%86%5E%28-1%29%29+%5D+%2F+2
TEOREMA
1: TEOREMA DEL POLINOMIO MINIMAL AUREO PRIMO
Las 8 isometrías áureas
primas corresponden a las raíces complejas del siguiente polinomio minimal:
1 - x2 + x4
– x6 + x8 = 0
https://www.wolframalpha.com/input/?i=%E2%88%91+n%3D0+to+4+%28-1%29%5En+x%5E%282n%29
https://www.wolframalpha.com/input/?i=1+-+x%5E2+%2B+x%5E4+-+x%5E6+%2B+x%5E8+%3D+0
Ahora veamos
las isometrías áureas primas complejas de la forma:
P1 ↔ {18°, 198°}
P3 ↔ {126°,
306°}
P7 ↔ {54°, 234°}
P9 ↔ {162°, 342°}
PRIMOS PENULT-IMPARES: (Primes congruent to 11,13,17,19 mód 20)
Son aquellos primos
cuyo penúltimo dígito es un número impar. Estos primos tienen 4 clases
residuales módulo 360 y son los ángulos: 18°,54°,126°,162°. Estos primos
siempre dan ángulos que se encuentran en el primer y segundo cuadrante del
plano cartesiano 0 < θ < π
P1 ↔ {18°}
11,31,71,131,151,191,211,251,271,311,331,431,491,571,631,691,751,811,911, 971…
P3 ↔ {126°}
13,53,73,113,173,193,233,293,313,353,373,433,593,613,653,673,733,773,853, 953…
P7 ↔ {54°}
17,37,97,137,157,197,257,277,317,337,397,457,557,577,617,677,757,797,857, 877,937,977,997…
P9 ↔ {162°}
19,59,79,139,179,199,239,359,379,419,439,479,499,599,619,659,719,739,839, 859,919…
PRIMOS PENULTI-PARES:
Son aquellos primos
cuyo penúltimo dígito es un número par. Estos primos tienen 4 clases residuales
módulo 360 y son los ángulos: 198°,234°,306°,342°. Estos primos siempre dan
ángulos que se encuentran en el tercer y cuarto cuadrante del plano cartesiano π < θ < 2π.
P1 ↔ {198°}
41,61,101,181,241,281,401,421,461,521,541,601,641,661,701,761,821,881,941…
P3 ↔ {306°}
23,43,83,103,163,223,263,283,383,443,463,503,523,563,643,683,743,823,863, 883,983…
P7 ↔ {234°}
07,47,67,107,127,167,227,307,347,367,467,487,547,587,607,647,727,787,827, 887,907,947,967…
P9 ↔ {342°}
29,89,109,149,229,269,349,389,409,449,509,569,709,769,809,829,929…
Ver acá y acá
los ejemplos en Wolfram:
Cos18° = Cos342° = 0.9510…
Cos162° = Cos198°
= -0.9510…
Y en general:
Cos [ 2 32n
]° =
0.9510…si n es
impar =
[ root(2+φ) ] / 2
-0.9510…si n es
par =
- [ root(2+φ) ] / 2
Cos54° = Cos306° = 0.5877…
Cos126° = Cos234°
= -0.5877…
Y en general:
Cos [ 2 32n+1
]° =
0.5877…si n es
impar =
[ root(2 - φ^(-1)) ] / 2
-0.5877…si n es
par = - [ root(2 - φ^(-1)) ] / 2
PRIMOS PENULTI-IMPARES
i^(1/5) = Cos[
(2) 3^(2(67))° ] + i Sin[ 2((31))^(-1)(10^((31)-1) -1)° ]
i^(7/5) = Cos[
(2) 3^(2(52)+1)° ] + i Sin[2((13))^(-1)(10^((13)-1) -1)°]
i^(3/5) = Cos[ (2) 3^(2(53)+1)° ] + i
Sin[2((137))^(-1)(10^((137)-1) -1)°]
i^(9/5) = Cos[ (2) 3^(2(52))° ] + i
Sin[2((59))^(-1)(10^((59)-1) -1)°]
IGUALDAD ENTRE LAS RAÍCES COMPLEJAS
i-1/5 =
-i9/5
i-3/5 =
-i7/5
i-7/5 =
-i3/5
i-9/5 = -i1/5
PRIMOS PENULTI-PARES
-i^(1/5) = Cos[ (2) 3^(2(64))° ] + i
Sin[2((101))^(-1)(10^((101)-1) -1)°]
-i^(3/5) = Cos[ (2) 3^(2(62)+1)° ] +
i Sin[2((23))^(-1)(10^((23)-1) -1)°]
-i^(7/5) = Cos[ (2) 3^(2(67)+1)° ] +
i Sin[2((67))^(-1)(10^((67)-1) -1)°]
-i^(9/5) = Cos[ (2) 3^(2(67))° ] + i
Sin[2((109))^(-1)(10^((109)-1) -1)°]
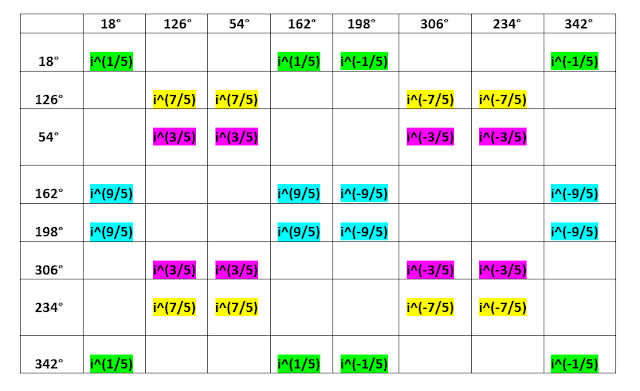
En el plano
complejo existen 8 raíces quintas que son isomorfas a 8 clases primas áureas
Estas imágenes
son:
i^(1/5)
i^(3/5)
i^(7/5)
i^(9/5)
i^(-1/5)
i^(-3/5)
i^(-7/5)
i^(-9/5)
Cos(18)° + i Sin(18)° = i^(1/5) P1 impar
Cos(54)° + i Sin(54)° = i^(3/5) P7 impar
Cos(126)°
+ i Sin(126)° = i^(7/5) P3 impar
Cos(162)°
+ i Sin(162)° = i^(9/5) P9 impar
Cos(198)°
+ i Sin(198)° = i^(-9/5) P1 par
Cos(234)°
+ i Sin(234)° = i^(-7/5) P7 par
Cos(306)°
+ i Sin(306)° = i^(-3/5) P3 par
Cos(342)° + i Sin(342)° = i^(-1/5) P9 par
i^(1/5) = Cos[ 2((971))^(-1)(10^((971)-1) -1) ]° + i
Sin[ 2((859))^(-1)(10^((859)-1) -1) ]°
-i^(7/5) = Cos[ 2((137))^(-1)(10^((137)-1) -1) ]° + i
Sin[ 2((43))^(-1)(10^((43)-1) -1) ]°
Cos[
2((311))^(-1)(10^((311)-1) -1) ]° + i Sin[ 2((271))^(-1)(10^((271)-1) -1) ]° =
i^(1/5)
Cos[
2((53))^(-1)(10^((53)-1) -1) ]° + i Sin[ 2((233))^(-1)(10^((233)-1) -1) ]° =
i^(7/5)
i^(-9/5) = Cos[ 2((59))^(-1)(10^((59)-1) -1) ]° + i Sin[
2((29))^(-1)(10^((29)-1) -1) ]°
i^(3/5) = Cos[ 2((977))^(-1)(10^((977)-1) -1) ]° + i
Sin[ 2((613))^(-1)(10^((613)-1) -1) ]°
TEOREMA 2: TEOREMA DE MATRIZ DE ROTACIÓN ÁUREA PRIMA
Existen
matrices de rotación de simetría áurea prima, tal que su determinante es
siempre 1. Esto solo se cumple para primos de la misma familia y para las
potencias enteras de 2 y 3 en los cosenos.
TEOREMA DE GRISALES
Las
clases áureas primas son invariantes bajo isometrías locales.
PRIMOS PENULTI-IMPARES:
det [ { Cos[ 2 3^(2(67)) ]°, -Sin[ (2((911))^(-1)(10^((911)-1) -1)) ] }, { Sin[ (2((311))^(-1)(10^((311)-1) -1)) ] , Cos[ 2 3^(2(67)) ]° } ]
det [ { Cos[ 2
3^(2(67)+1) ]°, -Sin[ (2((113))^(-1)(10^((113)-1) -1)) ] }, { Sin[ (2((733))^(-1)(10^((733)-1) -1)) ] ,
Cos[ 2 3^(2(767)+1) ]° } ]
det [ { Cos[ 2
3^(2(83)+1) ]°, -Sin[ (2((137))^(-1)(10^((137)-1) -1)) ] }, { Sin[ (2((997))^(-1)(10^((997)-1) -1)) ] ,
Cos[ 2 3^(2(87)+1) ]° } ]
det [ { Cos[ 2
3^(2(186)) ]°, -Sin[ (2((599))^(-1)(10^((599)-1) -1)) ] }, { Sin[ (2((499))^(-1)(10^((499)-1) -1)) ] ,
Cos[ 2 3^(2(186)) ]° } ]
PRIMOS PENULTI-PARES
det [ { Cos[ 2
3^(2(186)) ]°, -Sin[ (2((941))^(-1)(10^((941)-1) -1)) ] }, { Sin[ (2((541))^(-1)(10^((541)-1) -1)) ] ,
Cos[ 2 3^(2(186)) ]° } ]
det [ { Cos[ 2
3^(2(186)+1) ]°, -Sin[ (2((443))^(-1)(10^((443)-1) -1)) ] }, { Sin[ (2((883))^(-1)(10^((883)-1) -1)) ] ,
Cos[ 2 3^(2(186)+1) ]° } ]
det [ { Cos[ 2
3^(2(176)+1) ]°, -Sin[ (2((727))^(-1)(10^((727)-1) -1)) ] }, { Sin[ (2((967))^(-1)(10^((967)-1) -1)) ] ,
Cos[ 2 3^(2(186)+1) ]° } ]
det [ { Cos[ 2
3^(2(346)) ]°, -Sin[ (2((409))^(-1)(10^((409)-1) -1)) ] }, { Sin[ (2((929))^(-1)(10^((929)-1) -1)) ] ,
Cos[ 2 3^(2(8714)) ]° } ]
MATRIZ DE ROTACIÓN EN R3
[ { 1, 0, 0
}, { 0, Cos[ 2 3^(2(78)) ]°, -Sin[
(2((311))^(-1)(10^((311)-1) -1)) ] }, { 0, Sin[ (2((131))^(-1)(10^((131)-1)
-1)) ] , Cos[ 2 3^(2(788))]° } ]
[ { 1, 0, 0 }, { 0, Cos[ 2 3^(2(246)+1) ]°, -Sin[
(2((613))^(-1)(10^((613)-1) -1)) ] }, { 0, Sin[ (2((593))^(-1)(10^((593)-1)
-1)) ] , Cos[ 2 3^(2(666)+1)]° } ]
[ { 1, 0, 0
}, { 0, Cos[ 2 3^(2(4678)+1) ]°, -Sin[
(2((577))^(-1)(10^((577)-1) -1)) ] }, { 0, Sin[ (2((677))^(-1)(10^((677)-1)
-1)) ] , Cos[ 2 3^(2(6678)+1)]° } ]
[ { 1, 0, 0 }, { 0, Cos[ (2) 3^(2(508)) ]°, -Sin[
(2((769))^(-1)(10^((769)-1) -1)) ] }, { 0, Sin[ (2((269))^(-1)(10^((269)-1)
-1)) ] , Cos[ (2) 3^(2(668))]° } ]
MATRICES DE RAÍCES IMAGINARIAS CON RADIO
PHI
determinant of [ { i^(7/5), -i^(9/5) } ,
{ i^(9/5) , i^(7/5) } ]
TEOREMA 3: TEOREMA DE LAS RAÍCES COMPLEJAS DE FIBONACCI
De
la misma manera que existen 8 clases residuales isométricas para los numeros
primos, tambien existen 4 clases residuales para los 12th numeros de Fibonacci.
En este punto, cabe resaltar que las restantes 4 isometrías no corresponden a
ningun numero de Fibonacci ni primo.
https://www.wolframalpha.com/input/?i=%E2%88%91+n%3D0+to+4+x%5E%28n%29
https://www.wolframalpha.com/input/?i=1+%2B+x+%2B+x%5E2+%2B+x%5E3+%2B+x%5E4+%3D+0
Dichas
rotaciones se ordenan de la siguiente manera:
F12{1,6}
≡ 144° (mód 360)
F12{2,7}
≡ 288° (mód 360)
F12{3,8}
≡ 72° (mód 360)
F12{4,9}
≡ 216° (mód 360)
Son las clases residuales módulo 360 de los 12th números de
Fibonacci. Y dichas clases son las isometrías del pentágono regular. El coseno
de cada 12th Fibonacci es igual a –φ/2
y φ-1/2
La notación F12{1,6}, significa que son los
12th Fibonacci cuya última cifra es 1 o 6. Y así para los demás.
Table [ ( Fib(12 n) ) mod360, { n, 1, 100, 1 } ]
Veamos acá y acá en Wolfram:
[ Fib(12 43) ] mód360 = 72
https://www.wolframalpha.com/input/?i=%5B+Fib%2812+43%29+%5D+mod360+%3D+72
[ Fib(12 541) ] mod360 = 144
https://www.wolframalpha.com/input/?i=%5B+Fib%2812+541%29+%5D+mod360+%3D+144
[ Fib(12 599) ] mod360 = 216
https://www.wolframalpha.com/input/?i=%5B+Fib%2812+599%29+%5D+mod360+%3D+216
[ Fib(12 47) ] mód360 = 288
https://www.wolframalpha.com/input/?i=%5B+Fib%2812+47%29+%5D+mod360+%3D+288
Table
[ ( Fib(12 n) ) mod360 = 72 , { n, 3, 200, 5 } ]
Table
[ ( Fib(12 n) ) mod360 = 144 , { n, 1, 200, 5 } ]
Table
[ ( Fib(12 n) ) mod360 = 216 , { n, 4, 200, 5 } ]
Table
[ ( Fib(12 n) ) mod360 = 288 , { n, 2, 200, 5 } ]
POLINOMIO MINIMAL DE 12TH FIBONACCI: 72, 144, 216, 288
1
+ x + x^2 + x^3 + x^4 = 0
https://www.wolframalpha.com/input/?i=1+%2B+x+%2B+x%5E2+%2B+x%5E3+%2B+x%5E4+%3D+0
∑
n=0 to 4 x^n
https://www.wolframalpha.com/input/?i=%E2%88%91+n%3D0+to+4+x%5En
POLINOMIO MINIMAL DE: 36, 108, 252, 324
1
- x + x^2 - x^3 + x^4 = 0
https://www.wolframalpha.com/input/?i=1+-+x+%2B+x%5E2+-+x%5E3+%2B+x%5E4+%3D+0
∑
n=0 to 4 (-1)^n x^n
https://www.wolframalpha.com/input/?i=%E2%88%91+n%3D0+to+4++%28-1%29%5En+x%5En
LAS 8 RAÍCES COMPLEJAS DE FIBONACCI
ISOMETRÍAS DE 12TH FIBONACCI:
72°
↔ 2π/5
144° ↔ 4π/5
216° ↔ 6π/5 ↔ -144° ↔ -4π/10
288° ↔ 8π/5 ↔ -72° ↔ -2π/10
36° ↔ π/5
108° ↔ 3π/5
252° ↔ 7π/5 ↔ -108° ↔ -3π/5
324° ↔ 9π/5 ↔ -36°
↔ -π/5
i2/5 = Cos36 + i Sin36
i4/5 = Cos72 + i Sin72
i6/5 = Cos108 + i Sin108
i8/5 = Cos144 + i Sin144
i-2/5 = - i8/5 = Cos324 + i Sin324
i-4/5 = - i6/5 = Cos288 + i Sin288
i-6/5 = - i4/5 = Cos252 + i Sin252
i-8/5 = - i2/5 = Cos216 + i Sin216
i^(4/5) =
Cos(72) + iSin (72)
https://www.wolframalpha.com/input/?i=i%5E%284%2F5%29+%3D++Cos%2872%29+%2B+iSin+%2872%29
i^(8/5) = Cos(144) + iSin(144)
https://www.wolframalpha.com/input/?i=+i%5E%288%2F5%29+%3D+Cos%28144%29+%2B+iSin%28144%29
- i^(6/5) = Cos(288) + iSin (288)
https://www.wolframalpha.com/input/?i=-+i%5E%286%2F5%29+%3D+Cos%28288%29+%2B+iSin+%28288%29
- i^(2/5) = Cos(216) + iSin (216)
https://www.wolframalpha.com/input/?i=-+i%5E%282%2F5%29+%3D+Cos%28216%29+%2B+iSin+%28216%29+
TEOREMA
DE RAÍCES QUINTAS DE FIBONACCI
Existen 4
ángulos áureos que están a 180 grados de las isometrías de Fibonacci. Estos ángulos son: 36°, 108°, 252°, 324°. Y corresponden a los vértices de un
pentágono rotado 180° en sentido horario con respecto al pentágono de los Fibonacci.
216° - 180°
= 36°
288° - 180°
= 108°
72° + 180°
= 252°
144° + 180°
= 324°
F12k{1,6} ≡ 144° (mód 360)
F12k{2,7} ≡ 288° (mód 360)
F12k{3,8} ≡ 72° (mód 360)
F12k{4,9} ≡ 216° (mód 360)
Cos(36)° + i Sin(36)° = i^(2/5) F12k(6)-pi
Cos(72)° + i Sin(72)° = i^(4/5) F12k(2)
Cos(108)°
+ i Sin(108)° = i^(6/5) F12k(8)-pi
Cos(144)°
+ i Sin(144)° = i^(8/5) F12k(4)
Cos(216)°
+ i Sin(216)° = i^(-8/5) F12k(6)
Cos(252)°
+ i Sin(252)° = i^(-6/5) F12k(2)-pi
Cos(288)°
+ i Sin(288)° = i^(-4/5) F12k(8)
Cos(324° + i Sin(324)° = i^(-1/5) F12k(4)-pi
Ángulos
Fibonacci
i^(-4/5) = Cos [ Fib (12 43) ]° + i Sin [ Fib (12 48) - 180 ]°
i^(6/5) = Cos [ Fib (12 43) -180 ]° + i Sin [ Fib (12 48) ]°
i^(-8/5) = Cos [ Fib (12 44) ]° + i
Sin [ Fib (12 49) ]°
i^(-2/5) = Cos [ Fib (12 49) -180 ]°
+ i Sin [ Fib (12 46) -180 ]°
i^(2/5) =
Cos(36) + iSin (36)
https://www.wolframalpha.com/input/?i=i%5E%282%2F5%29+%3D++Cos%2836%29+%2B+iSin+%2836%29
i^(6/5) = Cos(108) + iSin (108)
https://www.wolframalpha.com/input/?i=+i%5E%286%2F5%29+%3D+Cos%28108%29+%2B+iSin+%28108%29
i^(-6/5) = Cos (252) + i Sin (252)
https://www.wolframalpha.com/input/?i=+i%5E%28-6%2F5%29+%3D+Cos%28252%29+%2B+iSin+%28252%29
i^(-2/5) = Cos (324) + i Sin (324)
https://www.wolframalpha.com/input/?i=+i%5E%28-2%2F5%29+%3D+Cos+%28324%29+%2B+i+Sin+%28324%29
https://www.wolframalpha.com/input/?i=+i%5E%282%2F5%29+%3D+cos36+%2B+i+sin144
i^(-2/5) = cos36 + i sin216
https://www.wolframalpha.com/input/?i=+i%5E%28-2%2F5%29+%3D+cos36+%2B+i+sin216
i^(-2/5) = cos36 + i sin324
https://www.wolframalpha.com/input/?i=+i%5E%28-2%2F5%29+%3D+cos36+%2B+i+sin324
i^(6/5) = cos108 + i sin72
Ángulo 36
i^(2/5) = Cos [ Fib (12 44) - 180 ]°
+ i Sin [ Fib (12 49) - 180 ]°
Ángulo 108
i^(6/5) = Cos [ Fib (12 42) - 180 ]°
+ i Sin [ Fib (12 47) - 180 ]°
Ángulo 252
i^(-6/5) = Cos [ Fib (12 43) - 180 ]°
+ i Sin [ Fib (12 48) - 180 ]°
Ángulo 324
i^(-2/5) = Cos [ Fib (12 41) - 180 ]°
+ i Sin [ Fib (12 46) - 180 ]°
RAÍCES COMPLEJAS ÁUREAS DE 12TH FIBONACCI
- i^(2/5) = Cos [ Fib (12 44) ]° + i Sin [ Fib (12 44) ]°
i^(-8/5) = Cos [ Fib (12 4554) ]° + i Sin [ Fib (12 4474) ]°
i^(-8/5) = Cos [ Fib (12 459) ]° + i Sin [ Fib (12 479) ]°
i^(4/5) = Cos [ Fib (12 13) ]° + i Sin [ Fib (12 23) ]°
i^(8/5) = Cos [ Fib (12 101) ]° + i Sin [ Fib (12 551) ]°
-i^(6/5) = Cos [ Fib (12 532) ]° + i Sin [ Fib (12 22) ]°
i^(-4/5) = Cos [ Fib (12 532) ]° + i Sin [ Fib (12 32) ]°
Table [ ( 2^(2n-1) 3^(2n+1) ) mod 360 = 144 , { n, 2, 100, 1 } ]
MATRIZ DE ROTACIÓN DE FIBONACCI 12TH
El determinante de las matrices de 12th Fibonacci es 1.
det [ { Cos [ Fib (12 31) ]°, -Sin [ Fib (12 31)] }, { Sin [ Fib (12 76) ] , Cos [ Fib (12 76) ] }
]
det [ { Cos [ Fib (12 32) ]°, -Sin [ Fib (12 37)] }, { Sin [ Fib (12 72) ] , Cos [ Fib (12 77) ] }
]
det [ { Cos [ Fib (12 43) ]°, -Sin [ Fib (12 18)] }, { Sin [ Fib (12 733) ] , Cos [ Fib (12 118) ]
} ]
det [ { Cos [ Fib (12 94) ]°, -Sin [ Fib (12 19)] }, { Sin [ Fib (12 74) ] , Cos [ Fib (12 29) ] }
]
LA TRAZA ES EL NÚMERO ÁUREO Y SU
INVERSO MULTIPLICATIVO:
[ { Cos [ Fib (12 91)
]°, -Sin [ Fib (12 11)] }, { Sin [ Fib
(12 76) ] , Cos [ Fib (12 26) ] } ]
[ { Cos [ Fib (12 94)
]°, -Sin [ Fib (12 19)] }, { Sin [ Fib
(12 74) ] , Cos [ Fib (12 29) ] } ]
[ { Cos [ Fib (12 93)
]°, -Sin [ Fib (12 13)] }, { Sin [ Fib
(12 78) ] , Cos [ Fib (12 28) ] } ]
[ { Cos [ Fib (12 92)
]°, -Sin [ Fib (12 922)] }, { Sin [ Fib
(12 77) ] , Cos [ Fib (12 27) ] } ]
MATRIZ DE ROTACIÓN DE ÁNGULOS NO ASOCIADOS:
det [ { Cos
[ 36 ]°, -Sin [ 36 ] }, { Sin [ 36 ]° ,
Cos [ 36 ]° } ]
det [ { Cos
[ 108 ]°, -Sin [ 108 ] }, { Sin [ 108 ]°
, Cos [ 108 ]° } ]
det [ { Cos [ 252 ]°, -Sin [ 252 ] }, { Sin [ 252 ]° , Cos [ 252 ]° } ]
det [ { Cos
[ 324 ]°, -Sin [ 324 ] }, { Sin [ 324 ]°
, Cos [ 324 ]° } ]
TEOREMA DEL COCIENTE HIPERBÓLICO ÁUREO PRIMO
El cociente
del seno hiperbólico entre el coseno hiperbólico de mi función áurea prima
da como resultado 8 imágenes exponenciales áureas que son las distintas
combinaciones de las 8 familias disjuntas de números primos.
Haciendo una
tabla 8x8 para las imágenes, de tal manera, que las clases primas de la columna
sean el numerador y las clases primas de las filas sean el denominador, se
obtienen los siguientes resultados generales.
Las 8 imágenes son:
[ e^(φ) - e^(-φ) ] / [ e^(φ) + e^(-φ) ]
[ e^(-φ) - e^(φ) ] / [ e^(φ) + e^(-φ)
]
[
e^(-φ) - e^(φ) ] / [ e^(1/φ) + e^(-1/φ) ]
[
e^(φ) - e^(-φ) ] / [ e^(1/φ) + e^(-1/φ) ]
[ e^(1/φ)
- e^(-1/φ) ] / [ e^(φ) + e^(-φ) ]
[
e^(-1/φ) - e^(1/φ) ] / [ e^(φ) + e^(-φ) ]
[ e^(1/φ) - e^(-1/φ) ] / [ e^(1/φ) +
e^(-1/φ) ]
[ e^(-1/φ) - e^(1/φ) ] / [ e^(1/φ) +
e^(-1/φ) ]
|
|
P1 impar |
P3impar |
P7impar |
P9 impar |
P1 par |
P3 par |
P7 par |
P9 par |
|
P1 impar |
[
e^(1/φ) - e^(-1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[e^(1/φ) - e^(-1/φ) ] / [e^(φ) + e^(-φ)] |
[e^(1/φ) - e^(-1/φ) ] / [e^(φ) + e^(-φ)] |
[
e^(1/φ) - e^(-1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[
e^(1/φ) - e^(-1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[e^(1/φ) - e^(-1/φ) ] / [e^(φ) + e^(-φ)] |
[e^(1/φ) - e^(-1/φ) ] / [e^(φ) + e^(-φ)] |
[
e^(1/φ) - e^(-1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
|
P3 impar |
[ e^(φ) - e^(-φ) ] / [e^(-1/φ) + e^(1/φ)] |
[
e^(φ) - e^(-φ) ] / [ e^(φ) + e^(-φ) ] |
[
e^(φ) - e^(-φ) ] / [ e^(φ) + e^(-φ) ] |
[ e^(φ) - e^(-φ) ] / [e^(-1/φ) + e^(1/φ)] |
[ e^(φ) - e^(-φ) ] / [e^(-1/φ) + e^(1/φ)] |
[
e^(φ) - e^(-φ) ] / [ e^(φ) + e^(-φ) ] |
[
e^(φ) - e^(-φ) ] / [ e^(φ) + e^(-φ) ] |
[ e^(φ) - e^(-φ) ] / [e^(-1/φ) + e^(1/φ)] |
|
P7 impar |
[ e^(φ) - e^(-φ) ] / [e^(-1/φ) + e^(1/φ)] |
[
e^(φ) - e^(-φ) ] / [ e^(φ) + e^(-φ) ] |
[
e^(φ) - e^(-φ) ] / [ e^(φ) + e^(-φ) ] |
[ e^(φ) - e^(-φ) ] / [e^(-1/φ) + e^(1/φ)] |
[ e^(φ) - e^(-φ) ] / [e^(-1/φ) + e^(1/φ)] |
[
e^(φ) - e^(-φ) ] / [ e^(φ) + e^(-φ) ] |
[
e^(φ) - e^(-φ) ] / [ e^(φ) + e^(-φ) ] |
[ e^(φ) - e^(-φ) ] / [e^(-1/φ) + e^(1/φ)] |
|
P9 impar |
[
e^(1/φ) - e^(-1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[e^(1/φ) - e^(-1/φ) ] / [e^(φ) + e^(-φ)] |
[e^(1/φ) - e^(-1/φ) ] / [e^(φ) + e^(-φ)] |
[
e^(1/φ) - e^(-1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[
e^(1/φ) - e^(-1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[e^(1/φ) - e^(-1/φ) ] / [e^(φ) + e^(-φ)] |
[e^(1/φ) - e^(-1/φ) ] / [e^(φ) + e^(-φ)] |
[
e^(1/φ) - e^(-1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
|
P1 par |
[
e^(-1/φ) - e^(1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[ e^(-1/φ) - e^(1/φ) ] / [e^(φ) +
e^(-φ)] |
[ e^(-1/φ) - e^(1/φ) ] / [e^(φ) +
e^(-φ)] |
[
e^(-1/φ) - e^(1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[
e^(-1/φ) - e^(1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[ e^(-1/φ) - e^(1/φ) ] / [e^(φ) +
e^(-φ)] |
[ e^(-1/φ) - e^(1/φ) ] / [e^(φ) +
e^(-φ)] |
[
e^(-1/φ) - e^(1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
|
P3 par |
[ e^(-φ) - e^(φ) ] / [e^(-1/φ) +
e^(1/φ)] |
[
e^(-φ) - e^(φ) ] / [ e^(φ) + e^(-φ) ] |
[
e^(-φ) - e^(φ) ] / [ e^(φ) + e^(-φ) ] |
[ e^(-φ) - e^(φ) ] / [e^(-1/φ) +
e^(1/φ)] |
[ e^(-φ) - e^(φ) ] / [e^(-1/φ) +
e^(1/φ)] |
[
e^(-φ) - e^(φ) ] / [ e^(φ) + e^(-φ) ] |
[
e^(-φ) - e^(φ) ] / [ e^(φ) + e^(-φ) ] |
[ e^(-φ) - e^(φ) ] / [e^(-1/φ) +
e^(1/φ)] |
|
P7 par |
[ e^(-φ) - e^(φ) ] / [e^(-1/φ) +
e^(1/φ)] |
[
e^(-φ) - e^(φ) ] / [ e^(φ) + e^(-φ) ] |
[
e^(-φ) - e^(φ) ] / [ e^(φ) + e^(-φ) ] |
[ e^(-φ) - e^(φ) ] / [e^(-1/φ) +
e^(1/φ)] |
[ e^(-φ) - e^(φ) ] / [e^(-1/φ) +
e^(1/φ)] |
[
e^(-φ) - e^(φ) ] / [ e^(φ) + e^(-φ) ] |
[
e^(-φ) - e^(φ) ] / [ e^(φ) + e^(-φ) ] |
[ e^(-φ) - e^(φ) ] / [e^(-1/φ) +
e^(1/φ)] |
|
P9 par |
[
e^(-1/φ) - e^(1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[ e^(-1/φ) - e^(1/φ) ] / [e^(φ) +
e^(-φ)] |
[ e^(-1/φ) - e^(1/φ) ] / [e^(φ) +
e^(-φ)] |
[
e^(-1/φ) - e^(1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[
e^(-1/φ) - e^(1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
[ e^(-1/φ) - e^(1/φ) ] / [e^(φ) +
e^(-φ)] |
[ e^(-1/φ) - e^(1/φ) ] / [e^(φ) +
e^(-φ)] |
[
e^(-1/φ) - e^(1/φ) ] / [ e^(1/φ) + e^(-1/φ) ] |
Sinh[ 2sin[ (2((11))^(-1)(10^((11)-1) -1)) ]° ] / Cosh[ 2sin[ (2((31))^(-1)(10^((31)-1) -1)) ]° ] = [ e^(1/φ) - e^(-1/φ) ] / [ e^(1/φ) + e^(-1/φ) ]
Sinh[ 2sin[ (2((13))^(-1)(10^((13)-1) -1)) ]° ] / Cosh[ 2sin[ (2((53))^(-1)(10^((53)-1) -1)) ]° ] = [ e^(φ) - e^(-φ) ] / [ e^(φ) + e^(-φ) ]
Sinh[ 2sin[ (2((103))^(-1)(10^((103)-1) -1)) ]° ] / Cosh[ 2sin[ (2((13))^(-1)(10^((13)-1) -1)) ]° ] = [ e^(-φ) - e^(φ) ] / [ e^(φ) + e^(-φ) ]
Sinh[ 2sin[ (2((103))^(-1)(10^((103)-1) -1)) ]° ] / Cosh[ 2sin[ (2((11))^(-1)(10^((11)-1) -1)) ]° ] = [ e^(-φ) - e^(φ) ] / [ e^(-1/φ) + e^(1/φ) ]
Sinh[ 2sin[ (2((109))^(-1)(10^((109)-1) -1)) ]° ] / Cosh[ 2sin[ (2((17))^(-1)(10^((17)-1) -1)) ]° ] = [ e^(-1/φ) - e^(1/φ) ] / [e^(φ) + e^(-φ)]
TEOREMA
EXPONENCIAL ÁUREO PRIMO
La funcion
exponencial ex se puede expresar como la suma del seno hiperbólico y
del coseno hiperbólico
Sinh(x) +
Cosh(x) = e^x
Si
reemplazamos la variable x, en mi función áurea prima se obtienen 8 imágenes áureas
unicas para cada una de las 8 clases residuales o familias disjuntas primas.
e^(φ)
e^(-φ)
e^(1/φ)
e^(-1/φ)
(1/2) [ -e^(φ) + e^(-φ) + e^(1/φ) + e^(-1/φ) ]
(1/2) [ e^(φ) - e^(-φ) + e^(1/φ) + e^(-1/φ) ]
(1/2) [ e^(φ) +
e^(-φ) - e^(1/φ) + e^(-1/φ) ]
(1/2)
[ e^(φ) + e^(-φ) + e^(1/φ) - e^(-1/φ) ]
|
|
P1 impar |
P3impar |
P7impar |
P9 impar |
P1 par |
P3 par |
P7 par |
P9 par |
|
P1 impar |
e^(1/φ) |
(1/2) [ e^(φ) + e^(-φ) + e^(1/φ) -
e^(-1/φ) ] |
(1/2) [ e^(φ) + e^(-φ) + e^(1/φ) -
e^(-1/φ) ] |
e^(1/φ) |
e^(1/φ) |
(1/2) [
e^(φ) + e^(-φ) + e^(1/φ) - e^(-1/φ) ] |
(1/2) [
e^(φ) + e^(-φ) + e^(1/φ) - e^(-1/φ) ] |
e^(1/φ) |
|
P3 impar |
(1/2) [ e^(φ) -
e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
e^(φ) |
e^(φ) |
(1/2) [ e^(φ) -
e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
(1/2) [ e^(φ) -
e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
e^(φ) |
e^(φ) |
(1/2) [ e^(φ) -
e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
|
P7 impar |
(1/2) [ e^(φ) -
e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
e^(φ) |
e^(φ) |
(1/2) [ e^(φ) -
e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
(1/2) [ e^(φ) -
e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
e^(φ) |
e^(φ) |
(1/2) [ e^(φ) -
e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
|
P9 impar |
e^(1/φ) |
(1/2) [
e^(φ) + e^(-φ) + e^(1/φ) - e^(-1/φ) ] |
(1/2) [
e^(φ) + e^(-φ) + e^(1/φ) - e^(-1/φ) ] |
e^(1/φ) |
e^(1/φ) |
(1/2) [
e^(φ) + e^(-φ) + e^(1/φ) - e^(-1/φ) ] |
(1/2) [
e^(φ) + e^(-φ) + e^(1/φ) - e^(-1/φ) ]] |
e^(1/φ) |
|
P1 par |
e^(-1/φ) |
(1/2) [ e^(φ) +
e^(-φ) - e^(1/φ) + e^(-1/φ) ] |
(1/2) [ e^(φ) +
e^(-φ) - e^(1/φ) + e^(-1/φ) ] |
e^(-1/φ) |
e^(-1/φ) |
(1/2) [ e^(φ) +
e^(-φ) - e^(1/φ) + e^(-1/φ) ] |
(1/2) [ e^(φ) +
e^(-φ) - e^(1/φ) + e^(-1/φ) ] |
e^(-1/φ) |
|
P3 par |
(1/2) [
-e^(φ) + e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
e^(-φ) |
e^(-φ) |
(1/2) [
-e^(φ) + e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
(1/2) [
-e^(φ) + e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
e^(-φ) |
e^(-φ) |
(1/2) [
-e^(φ) + e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
|
P7 par |
(1/2) [
-e^(φ) + e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
e^(-φ) |
e^(-φ) |
(1/2) [
-e^(φ) + e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
(1/2) [
-e^(φ) + e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
e^(-φ) |
e^(-φ) |
(1/2) [
-e^(φ) + e^(-φ) + e^(1/φ) + e^(-1/φ) ] |
|
P9 par |
e^(-1/φ) |
(1/2) [ e^(φ) +
e^(-φ) - e^(1/φ) + e^(-1/φ) ] |
(1/2) [ e^(φ) +
e^(-φ) - e^(1/φ) + e^(-1/φ) ] |
e^(-1/φ) |
e^(-1/φ) |
(1/2) [ e^(φ) +
e^(-φ) - e^(1/φ) + e^(-1/φ) ] |
(1/2) [ e^(φ) +
e^(-φ) - e^(1/φ) + e^(-1/φ) ] |
e^(-1/φ) |
Sinh[ 2sen[
(2((241))^(-1)(10^((241)-1) -1)) ]° ] + Cosh[ 2sen[ (2((691))^(-1)(10^((691)-1)
-1)) ]° ] = e^(-1/φ)
Sinh[ 2sen[
(2((503))^(-1)(10^((503)-1) -1)) ]° ] + Cosh[ 2sen[ (2((929))^(-1)(10^((929)-1)
-1)) ]° ] = (1/2) [ e^-φ + e^(-1/φ) + e^(1/φ) - e^φ ]
Sinh[ 2sen[
(2((101))^(-1)(10^((101)-1) -1)) ]° ] + Cosh[ 2sen[ (2((13))^(-1)(10^((13)-1)
-1)) ]° ] = (1/2) [ e^-φ + e^(-1/φ) - e^(1/φ) + e^φ ]
Sinh[ 2sen[
(2((107))^(-1)(10^((107)-1) -1)) ]° ] + Cosh[ 2sen[ (2((101))^(-1)(10^((101)-1)
-1)) ]° ] = (1/2) [ e^-φ + e^(-1/φ) + e^(1/φ) - e^φ ]
PRIMOS PENULTIMPARES (Primes congruent to 11,13,17,19 mod 20)
http://oeis.org/search?q=11%2C31%2C71%2C131%2C151%2C191%2C211%2C&sort=&language=&go=Search
http://oeis.org/search?q=13%2C53%2C73%2C113%2C173%2C193%2C233%2C293%2C313&sort=&language=&go=Search
https://www.wolframalpha.com/input/?i=Select%5BRange%5B11%2C+5000%2C+20%5D%2C+PrimeQ%5B%23%5D%26%5D
https://www.wolframalpha.com/input/?i=Select%5BRange%5B13%2C+5000%2C+20%5D%2C+PrimeQ%5B%23%5D%26%5D
https://www.wolframalpha.com/input/?i=Select%5BRange%5B17%2C+5000%2C+20%5D%2C+PrimeQ%5B%23%5D%26%5D
https://www.wolframalpha.com/input/?i=Select%5BRange%5B19%2C+5000%2C+20%5D%2C+PrimeQ%5B%23%5D%26%5D
PRIMOS PENULTIPARES (Primes congruent
to 1,3,7,9 mod 20)
http://oeis.org/search?q=7%2C47%2C67%2C107%2C127%2C167%2C227%2C307%2C347&sort=&language=&go=Search
http://oeis.org/search?q=29%2C89%2C109%2C149%2C229%2C269%2C349%2C389&sort=&language=&go=Search
https://www.wolframalpha.com/input/?i=Select%5BRange%5B1%2C+5000%2C+20%5D%2C+PrimeQ%5B%23%5D%26%5D
https://www.wolframalpha.com/input/?i=Select%5BRange%5B3%2C+2003%2C+20%5D%2C+PrimeQ%5B+%23+%5D%26%5D
https://www.wolframalpha.com/input/?i=Select%5BRange%5B7%2C+5000%2C+20%5D%2C+PrimeQ%5B%23%5D%26%5D
https://www.wolframalpha.com/input/?i=Select%5BRange%5B9%2C+5000%2C+20%5D%2C+PrimeQ%5B%23%5D%26%5D
BIBLIOGRAFÍA
Se encuentra ya
publicada en los 12 artículos anteriores en este sitio web

SUBGRUPO DE LIE: TEOREMA DE RAÍCES COMPLEJAS ÁUREAS PRIMAS Y TEOREMA MATRICIAL DE ROTACIÓN ÁUREA by JAVIER GRISALES HERRERA is licensed under a Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional License.
Creado a partir de la obra en http://javiermathprimes.blogspot.com/.
Puede hallar permisos más allá de los concedidos con esta licencia en http://javiermathprimes.blogspot.com/