DE UNA NUEVA FUNCIÓN ÁUREA PARA P PRIMO
JAVIER GRISALES HERRERA
«El problema de distinguir los números primos de los compuestos es
uno de los más importantes y útiles en aritmética. La dignidad de la
ciencia misma parece requerir que todos los medios posibles sean explorados
para resolver un problema tan elegante y célebre.» Carl Friedrich Gauss (1801).
Ya Euclides (c.300-265 a.C) en su obra Los Elementos,
definición III del libro VI, definió al número
áureo Phi así: "Se dice que una
recta ha sido cortada en extrema y media razón cuando la recta entera es al
segmento mayor como el segmento mayor es al segmento menor". De modo
que la longitud total de la recta dividida entre el segmento mayor sea igual al
segmento mayor dividido entre el segmento menor. Lo cual algebraicamente corresponde a la función x^2
–x -1 =0 y cuyas raíces son x= ϕ, y x= ϕ^-1. Entre muchas propiedades
interesantes asociadas a este número llamado ‘’el más irracional’’ que existe, se
suma el siguiente estudio desarrollado a partir de la trigonometría asociada y
al final mostraré una función identificadora de
números primos a partir del número áureo cuyo valor es:
(a+b)/a = a/b = ϕ
ϕ = (1+root 5
)/2 = 1,61803398874989484820458683436563811772030917980576…
1. NÚMERO ÁUREO EN LA TRIGONOMETRIA
El número áureo puede hallarse trigonométricamente mediante los senos y cosenos de ángulos enteros que cumplan la siguiente propiedad modular:
Proposición 1.1. Todo ángulo entero n si n = par y, n mod
9= 0, cuando n mod 5 es distinto de 0, está
relacionado con el número áureo φ
TABLA 1.1 Ángulos n mod 9 = 0 cuando n= par asociados al número áureo ϕ
2 sen 18 = ϕ^-1
|
2 sen 198 = -ϕ^-1
|
2 cos 36
= ϕ/2
|
2 cos 216 = -ϕ/2
|
2 sen 54 = ϕ/2
|
2 sen 234 = -ϕ/2
|
2 cos 72
= ϕ^-1
|
2 cos 252 = -ϕ^-1
|
2 cos 108
= -ϕ^-1
|
2 cos 288 = ϕ^-1
|
2 sen 126 = ϕ/2
|
2 sen 306 = -ϕ/2
|
2 cos 144 = -ϕ/2
|
2 cos 324 = ϕ/2
|
2 sen 162 = ϕ^-1
|
2 sen 342 = -ϕ^-1
|
Demostración 1.1: considérese un ángulo de la forma 9n siendo n = par,
se verifica que el seno y el coseno de ángulos de la forma 18n, si n mod 5 es
distinto de 0, calculan al número áureo.
Sea f(x) = 2cos (18n) y
f(x) = 2sen (18n), cuando n mod 5
es distinto de 0, se verifican únicamente las siguientes raíces como conjunto
solución: [ ϕ/2, -ϕ/2, ϕ^-1,
-ϕ^-1 ]
De acuerdo con la proposición 1.1 podemos concluir que
existe una asociación entre el número áureo y el
módulo 9, en el sistema decimal posicional.
Veamos algunos ejemplos particulares de la importancia del módulo 9 asociado a los ángulos que obtienen al número áureo como raíz en su estructura trigonométrica.
·
f(x) = Sen (321 - 123) = sen 198 = -ϕ^-1
·
f(x) = Sen (654 - 456) = sen 198 = -ϕ^-1
·
f(x) = Sen (987 – 789)= sen 198 = -ϕ^-1
·
f(x) = Sen (963 -369) = sen 594 = -ϕ/2
·
f(x) = Sen (852-258) = sen 594 =
-ϕ/2
·
f(x) = Sen (741-147) = sen 594 =
-ϕ/2
·
f(x) = Cos (396) = ϕ/2
·
f(x) = Cos (936) =
-ϕ/2
·
f(x) = Sen (333999666) = -ϕ/2
·
f(x) = Sen (999333666) = -ϕ/2
·
f(x) = Sen (666666666) = -ϕ/2
·
f(x) = Cos (987654321 – 123456789) = cos 864197532
= -ϕ^-1
f(x) = Cos (222444) = ϕ/2
f(x) = Cos (222444) = ϕ/2
Otro hallazgo fundamental que hice fue descubrir que
toda las potencias enteras de 6 también están relacionadas según el coseno del ángulo
dado con el número áureo.
Proposición 1.2: El coseno
del ángulo de toda potencia entera positiva de 6 es la mitad del número áureo expresada
así: f(x) = 2 cos(6^n) = -φ/2
, para cualquier n>1 (Ecuación 1).
Demostración 1.2: Sea f(x) = 2 cos(6^n)
= -ϕ/2 y n >1, donde n es un cualquier entero positivo y téngase en
cuenta que todas las potencias enteras de 6 son 0mod 9. Veamos los siguientes
ejemplos que son aplicables para cualquier entero positivo n:
f(x) = 2 cos(6^5) = cos (7776) = -ϕ/2
f(x) = 2 cos(6^14) = cos (78364164096) = -ϕ/2
f(x) = 2 cos(6^25) = cos (28430288029929701376) = -ϕ/2
Como vemos todos los ángulos cuyo módulo 9 sea 0, excepto aquellos que sean múltiplos de 5 y todas las potencias enteras de 6 están asociadas definitivamente al número áureo Phi. Ahora bien, mostraré que también esto se cumple para los Números Primos.
2. FUNCIÓN ÁUREA PARA P PRIMO
Todo número entero positivo p es primo sí y solo sí la suma de sus divisores propios es p+1 y he descubierto que están relacionados con el número áureo a través de sus periodos decimales recíprocos 1/p de modo que pueden ser identificados en el infinito a través del módulo 9.
Todo número entero positivo p es primo sí y solo sí la suma de sus divisores propios es p+1 y he descubierto que están relacionados con el número áureo a través de sus periodos decimales recíprocos 1/p de modo que pueden ser identificados en el infinito a través del módulo 9.
Proposición 2.1: Todo número
primo p>5 cumple que el periodo decimal de su recíproco de la forma 1/p es 0
mod 9 según el teorema de Midy. A partir de lo cual, se puede formalizar una
función áurea de números primos cuyas raíces son el número áureo.
Demostración 2.1: obténgase el periodo decimal del recíproco de
cualquier número primo p>5, empezando por el numero 7 cuyo periodo decimal
corresponde a ‘’142857’’, los cuales por el Teorema de Midy que nos dice: Sea a/p una fracción donde a<p y p>5 es un numero primo. Suponga ademas que esta fracción tiene una expansión decimal periódica, donde la cantidad de dígitos en el periodo es par, esto es: a/p = 0, a1a2a3...a2k-1 a2k Si dividimos el periodo en dos mitades (los primeros 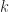 1 y los últimos
1 y los últimos 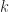 2, a esta acción la llamaremos dividir en bloques) y los sumamos, obtenemos un número que consiste en solo nueves.
2, a esta acción la llamaremos dividir en bloques) y los sumamos, obtenemos un número que consiste en solo nueves.
(i.e) 142857 --> 142 + 857 = 999
1/7 = 0,142857142857142857142857,
1/11= 0,09090909090909090909090909090909
1/13 = 0,0769230769230769230769230769230...
1/17 = 0,05882352941176470588235294117647...
1/19 = 0,052631578947368421052631578947...
1/23 = 0,04347826086956521739130434782608695652173913…
1/29 = 0,03448275862068965517241379310344827586206896551724137931…
1/31 = 0,032258064516129032258064516129032258064516129….
Cada periodo decimal obtenido a partir de los inversos
de los números primos>5 son de la forma 0 mod9, (i.e: 142857 mod9 = 0). A
partir de esta conclusión, diseñe la siguiente fórmula trigonométrica que
identifica números primos, de modo que siempre que p sea primo, la función tiene como raíces
exactas [φ/2,
-φ/2, φ^-1, -φ^-1 ]
Función áurea de números primos:
F(p) = 2 sen [(2((p)^(-1)(10^((p)-1) -1)]
Ecuación 2
f(p)
= 2 sen [(2((7)^(-1)(10^((7)-1) -1))] = 1/2(-1 -root5)
f(p)
= 2 sen [(2((13)^(-1)(10^((13)-1) -1))] = 1/2(1+root5)
f(p)
= 2 sen [(2((19)^(-1)(10^((19)-1) -1))] = 1/2(root5 -1)
f(p) = 2 sen [(2((23)^(-1)(10^((23)-1) -1))] = 1/2(-1 -root5)
f(p) = 2 sen [(2((29)^(-1)(10^((29)-1) -1))] = 1/2(1-root5)
f(p) = 2 sen [(2((31)^(-1)(10^((31)-1) -1))] = 1/2(root5 -1)
Click Aquí:
De esta manera, verificamos que siempre que el número p sea primo la raíz de dicha función dorada será siempre el número áureo phi. Esto se cumple para todos los primos p≥7 y permite identificarlos eficazmente con exactitud matemática.
Apéndice dorado:
Sobre una nueva expresión para el
enésimo Fibonacci
F (n) =
round [ ϕ^(n) / sqrt5 ] ecuación 3
Esta expresión que encontré es mucho más simple y
eficiente que la fórmula de Binet para calcular exactamente al enésimo número de Fibonacci. Utilizando todas las potencias enteras positivas del numero áureo dividido entre su discriminante, es decir, la raíz cuadrada de 5.
Veamos algunos ejemplos para comprobarlo:
Veamos algunos ejemplos para comprobarlo:
F (n) = round [ ϕ^(6) / sqrt5 ] = 8
F (n) = round [ ϕ^(12) / sqrt5 ] = 144
F (n) = round [ ϕ^(14) / sqrt5 ] = 377
F (n) = round [ ϕ^(22) / sqrt5 ] = 17711
F (n) = round [ ϕ^(100) / sqrt5 ] = 354224848179261915075
Click Aquí:
Se puede verificar para cualquier n entero positivo aquí para encontrar el valor del enésimo número Fibonacci donde se puede obtener su cardinal a partir de su ordinal n.
De otro lado, añado también aquí esta nueva identidad para el número e (2,7182818284590452353602874713527…) que es base de los logaritmos naturales que descubrí gracias a las increíbles propiedades del número áureo que ofrecen otras posibilidades a la identidad de Euler:
e= (golden ratio(1-golden ratio))^1/ipi
haga click aquí:
De otro lado, añado también aquí esta nueva identidad para el número e (2,7182818284590452353602874713527…) que es base de los logaritmos naturales que descubrí gracias a las increíbles propiedades del número áureo que ofrecen otras posibilidades a la identidad de Euler:
e= (golden ratio(1-golden ratio))^1/ipi
haga click aquí:
https://www.wolframalpha.com/input/?i=e%3D+(golden+ratio(1-golden+ratio))%5E1%2Fipi
BIBLIOGRAFIA
1.
Gray,
Alexander J., "Digital roots and reciprocals of primes," Mathematical Gazette 84.09, March 2000, 86.
2.
Kak,
Subhash, Chatterjee, A. "On decimal sequences." IEEE Transactions on
Information Theory, vol. IT-27, pp. 647-652, September 1981.
3. Kalman, Dan; 'Fractions
with Cycling Digit Patterns' The College Mathematics Journal, Vol. 27, No. 2. (Mar., 1996), pp. 109–115.
5. Midy’s theorem for periodical decimals, Joseph Lewittes, Electronic Journal of Combinatorial
Number Theory, Vol. 7, (2007).
6. Decimal expansion of 1/p and subgroup sums, Ankit Gupta y B. Sury, Integers: Electronic Journal
of Combinatorial Number Theory, Vol. 5, (2005), A19.